终而复始

问题描述

青石板路的尽头堆满了财宝。小 L 感到很一阵阵失望，只能先搬走一部分财宝了。

财宝是一个个矩形紧紧挨在一起，第 $i$ 个矩形宽度为 $1$ ，高度是 $h_i$

小 L 是一个 不会贪心 不贪心的人，所以决定只拿走最大矩形的面积这么多。

拿着拿着，小 L 突然想到，其实这个财宝墙后面还是有路的。

输入格式

第一行一个整数 $n$ , $n\le 10^5$
第二行，一行数，第 $i$ 个数代表 $h_i$ , $0\le h_i\le 10^9$

输出格式

一行，一个数，代表最大矩形面积

样例输入

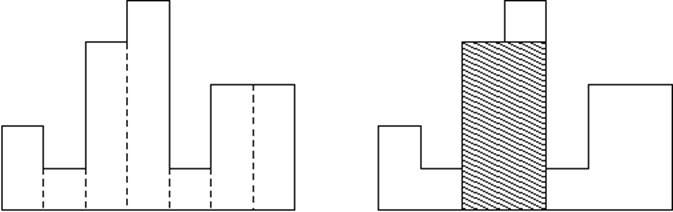
7
2 1 4 5 1 3 3 

样例输出

8

方法一

#include <bits/stdc++.h>
using namespace std;
#define ll long long

ll n, t, ans = 0;
vector<ll> h, l, r;
deque<pair<ll, ll>> s;  // hight,index

void dstack(vector<ll>& v) {  // 构建递减栈,栈顶是最大的,并且将每次栈顶的index(即左边第一个低于此处的矩形的index)存到v这个vector
    s.clear();
    ll i = 0;
    for (const auto& ele : h) {
        while (!s.empty() and s.back().first >= ele)
            s.pop_back();
        if (s.empty())
            v.emplace_back(-1);  // 左边都比自己高
        else
            v.emplace_back(s.back().second);
        s.emplace_back(ele, i++);
    }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i) {
        scanf("%lld", &t);
        h.emplace_back(t);
    }
    dstack(l);
    reverse(h.begin(), h.end());
    dstack(r);
    reverse(r.begin(), r.end());
    reverse(h.begin(), h.end());
    for (int i = 0; i < n; ++i) {
        /*ll li = l[i] + 1, ri = n - r[i] - 2;
        ans = max(ans, h[i] * (ri - li + 1));*/
        ans = max(ans, h[i] * (n - 2 - r[i] - l[i]));
    }
    cout << ans;
    return 0;
}

方法二

#include <bits/stdc++.h>
using namespace std;
#define ll long long

ll n, t, ans = 0;
vector<ll> h, disl, disr;
deque<pair<ll, ll>> s;  // hight,index

void dstack(vector<ll>& v) {  // 构建递减栈,栈顶是最大的,并且将每次左边第一个低于此处的矩形的右边的那个矩形距离存到v这个vector
    s.clear();
    ll i = 1;
    for (const auto& ele : h) {
        while (!s.empty() and s.back().first >= ele)
            s.pop_back();
        if (s.empty())
            v.emplace_back(i);  // 左边都比自己高
        else
            v.emplace_back(i - s.back().second);
        s.emplace_back(ele, i++);
    }
}

int main() {
    cin >> n;
    for (int i = 0; i < n; ++i) {
        scanf("%lld", &t);
        h.emplace_back(t);
    }
    dstack(disl);
    reverse(h.begin(), h.end());
    dstack(disr);
    reverse(h.begin(),h.end());
    reverse(disr.begin(), disr.end());
    for (int i = 0; i < n; ++i)
        ans = max(ans, h[i] * (disl[i] + disr[i] - 1));
    cout << ans;
    return 0;
}