斐波那契数列

题目描述

斐波那契数列的定义如下：

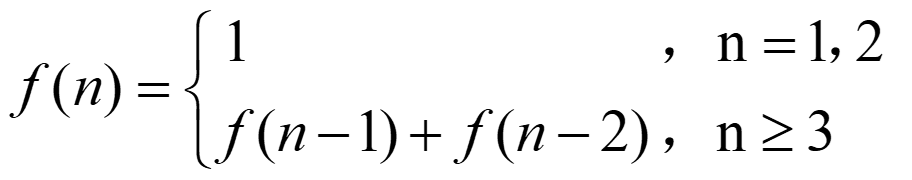
给出 $n,p$ ，求出 $f(n)\%p$ 的值。

输入格式

第一行一个数 $T(1\le T\le 100)$，表示数据组数。
接下来 $T$ 行，每行两个整数 $n,p(1\le n\le 10^9,10^8\le p\le 10^9)$。

输出格式

输出 $T$ 行，表示每组数据的答案。

测试用例

输入

6
1 998244353
2 998244353
3 998244353
4 998244353
5 998244353
1000000000  998244353

输出

1
1
2
3
5
990450892

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define MAXN 1000005

const ll N = 2;    //方阵的大小
ll mod = 1e9 + 7;  //模
struct Matrix {
    ll x[N][N];
    Matrix() {
        memset(x, 0, sizeof(x));
    }
    Matrix(const Matrix &b) {
        memcpy(x, b.x, sizeof(x));
    }
    Matrix operator*(const Matrix &b) const {
        Matrix c;
        for (ll i = 0; i < N; i++)
            for (ll j = 0; j < N; j++) {
                c.x[i][j] = 0;
                for (ll k = 0; k < N; k++) {
                    c.x[i][j] += x[i][k] * b.x[k][j] % mod;
                    c.x[i][j] %= mod;
                }
            }
        return c;
    }
};

Matrix fastpow(Matrix a, ll n) {
    Matrix res;
    for (ll i = 0; i < N; i++)
        res.x[i][i] = 1;
    while (n) {
        if (n & 1) res = res * a;
        a = a * a;
        n >>= 1;
    }
    return res;
}

int main() {
    ll t, n;
    cin >> t;
    Matrix a, b;
    a.x[0][0] = 1;
    a.x[0][1] = 1;
    a.x[1][0] = 1;
    a.x[1][1] = 0;

    for (ll i = 1; i <= t; ++i) {
        cin >> n >> mod;
        if (n > 2) {
            b = fastpow(a, n);
            cout << b.x[1][0] << "\n";
        } else {
            cout << 1 << "\n";
        }
    }

    return 0;
}